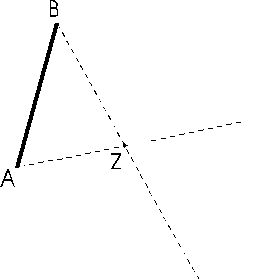3. Kongruenz

Von Bewegungen und Umklappungen als Abbildungen

Kongruenz wird als Deckungsgleichheit definiert - der Zusammenhang mit geometrischen Abbildungen wird herausgearbeitet, eine Übersicht über die Kongruenzabbildungen samt Querverbindungen zur Technik und zu den Ornament-gruppen rundet dieses Kapitel ab.

Das Umgehenkönnen und das Wissen über diese Kongruenzabbildungen benötigt man etwa bei den CAD-Programmen (v.a. im Fach GEOMETRISCHES ZEICHNEN).

A. Geometrische Abbildungen

Unter einer Abbildung versteht man eine eindeutige Zuordnung .

Jedem Punkt der Zeichenebene wird ein eindeutig bestimmter Punkt der Zeichenebene zugewiesen, jeder Figur eine Bildfigur.

Wir betrachten erstens nur umkehrbar eindeutige Abbildungen, zweitens in diesem Abschnitt nur solche Abbildungen, die die "Gestalt" einer Figur nicht ändern. So wie bei einer Axialspiegelung soll die Bildfigur etwa mit einer Schere aus dem Zeichenblatt ausgeschnitten und dann auf die Ausgangsfigur (Urfigur) so gelegt werden können, dass beide genau über-einanderliegen. Ur-und Bildfigur sollen "deckungsgleich" oder kongruent [ @] sein

Die betrachteten Abbildungen sind dann längentreu und winkeltreu (auch: flächentreu).

Sie heißen Kongruenzabbildungen!

Eigenschaften kongruenter Figuren F, F', F":

* F @ F reflexiv

* F @ F' Þ F' @ F symmetrisch

* F @ F' Ù F' @ F" Þ F @ F" transitiv

Die Kongruenz ist eine RST-Relation oder Äquivalenzrelation.

B. Fundamentalsatz

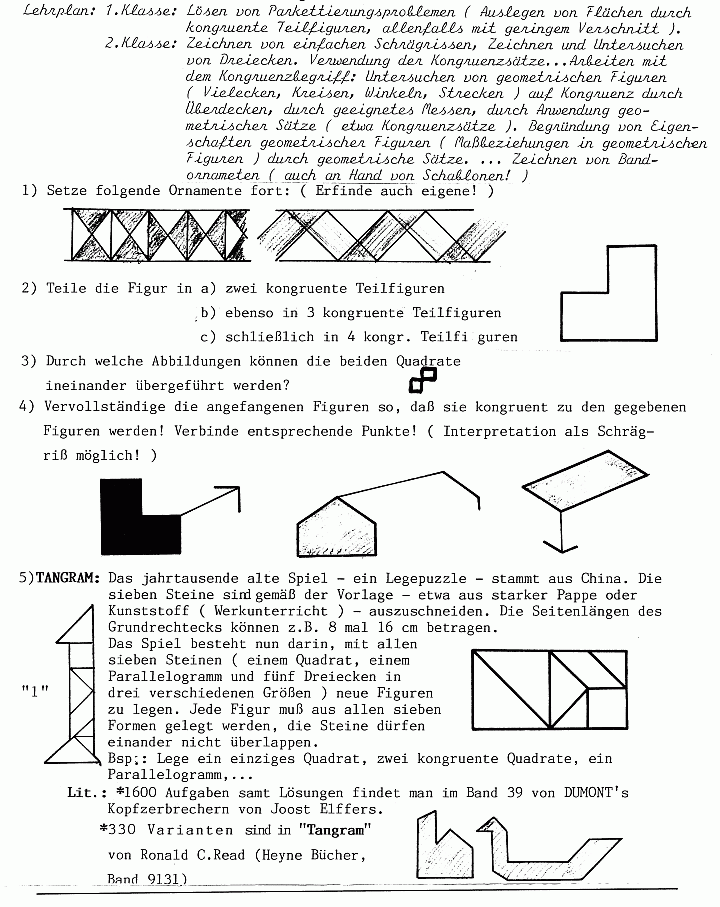
Wir machen ein Experiment:

1.Schritt:

Wir kopieren eine Punktmenge (z.B. Tintenspritzer) auf eine OH-Folie.

Falls der Kopierer keine echte Kopie machen kann (Längenverzerrungen v.a. in den Randbereichen), dann macht man am besten zwei Kopien, diese sind dann sicher deckungsgleich.

2. Schritt:

Die Folie wird auf das Original gelegt.

3. Schritt:

Wir bewegen die Folie über dem Original ein wenig - es entsteht ein Eindruck wie er in den folgenden Kopien wiedergegeben ist:

Was bedeutet dieses Ergebnis?

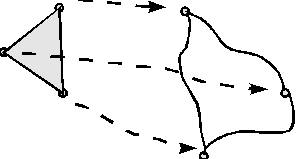
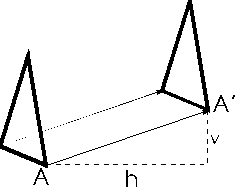
Wir vereinfachen zunächst: Statt der vielen Punkte betrachten wir nur noch je zwei Punkte A wird auf A' kopiert, B auf B'. Durch die Angabe zweier Punkte (A', B') ist die Folie der Lage nach eindeutig festgelegt. Um dies einzusehen stelle man sich etwa zwei Nadeln vor, mit denen man die Folie zunächst in A' fixiert (es sind nur noch Drehungen um A' möglich), dann in B'.

Nun lässt sich beweisen:

Irgendzwei Lagen eines bewegten ebenen Systems (z.B.: Original, Kopie) können stets durch eine Drehung (im Grenzfall durch eine Schiebung) auseinander hervorgehen!

Beweis:

Die Lagen seien durch je eine Strecke mit den Endpunkten AB und A'B' festgelegt. Wir setzen voraus, dass die Folie nur bewegt, nicht umgeklappt wurde!

Gibt es tatsächlich ein Drehzentrum Z, dann muss es von A und A' gleich weit weg sein, also auf der Streckensymmetralen von A und A' liegen, genauso für B und B'. Im Schnitt der Strecken-symmetralen liegt dann das Zentrum Z.

Haben die Streckensymmetralen in jedem Fall einen Schnittpunkt?

Fall 1: Sie könnten identisch sein.

Kann jetzt auch ein Drehzentrum Z gefunden werden?

......................................................................

Fall 2: Sie könnten parallel sein.

Dann müssen auch die Verbindungen ...... und ......... zueinander parallel sein.

Das Viereck ist dann wegen der Längengleichheit von AA' und BB' entweder ein gleichschenkeliges Trapez (siehe Fall 1) oder ein Parallelogramm (vgl. später). Im zweiten Fall kann AB in A'B' durch eine Schiebung transformiert werden!

Die große Bedeutung dieses Satzes liegt im Maschinenbau, dort heißt er Fundamentalsatz der ebenen Kinematik (= Lehre von der Bewegung starrer Systeme).

Fotos eines Müllcontainers: Die Abdeckung gelangt durch Drehung von einer Lage in die andere.

Ofenverschluss: Konstruiere das Drehzentrum von der geöffneten Lage in die verriegelte.

C. Drehung

Eine Drehung ist eine eindeutige, längen- und winkeltreue Abbildung der Ebene auf sich, wobei jeder Punkt der Ebene um ein gegebenes Zentrum Z um einen bestimmten Winkel in einem bestimmten Sinn (rechts , links) gedreht wird.

Angabe:

* Drehzentrum Z, Drehwinkel , Drehsinn

* 2 Paare von Punkten [(AA'),(BB')];

Z muss konstruiert werden,

Drehwinkel ergibt sich aus dem

Winkel Ð AZA'

Sorry, this page requires a Java-compatible web browser.

Beispiel: Anwendung bei einem Beweis.

Es gilt:

Der Höhenwinkel, unter dem der Polarstern über dem Horizont gesehen wird, stimmt mit der geographischen Breite des Beobachtungsstandortes überein.

Beweis:

Sorry, this page requires a Java-compatible web browser.

Weitere Eigenschaften der Drehung:

Eine Gerade g soll um ein Zentrum Z gedreht werden:

Es gilt:

Der Winkel zwischen g und g' stimmt mit dem Drehwinkel überein!

Fixelemente:

Fixpunkte: Bei allgemeinem Drehwinkel († 0°) gibt es nur einen Fixpunkt: ...........

Fixgeraden: Bei welchem Drehwinkel kann es Fixgerade geben? ..........

Fixkreise: ...........................................................................................

Spezialfall: Drehwinkel 180° (vgl E)

D. Schiebung oder Translation

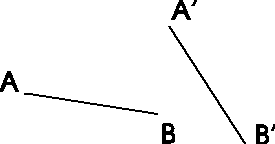
Eine Schiebung ist eine eindeutige, längen- und winkeltreue Abbildung der Ebene auf sich, wobei jeder Punkt der Ebene in eine gegebene Richtung gleich weit bewegt wird.

Angabe:

* Schiebungspfeil; alle Pfeile sind gleich lang, parallel und gleich orientiert;

auch durch ein Zahlenpaar (h/v) angebbar

Eine Menge von parallelen, gleich langen und gleich orientierten Pfeilen nennt man einen VEKTOR.

* Urpunkt und Bildpunkt

(legen Schiebungspfeil fest)

Beispiel: Das gegebene Trapez ist zu verschieben.

Beweis mit Hilfe einer Schiebung: Winkelsumme im Dreieck (vgl. später)

Fixelemente:

Fixpunkte

Fixgerade

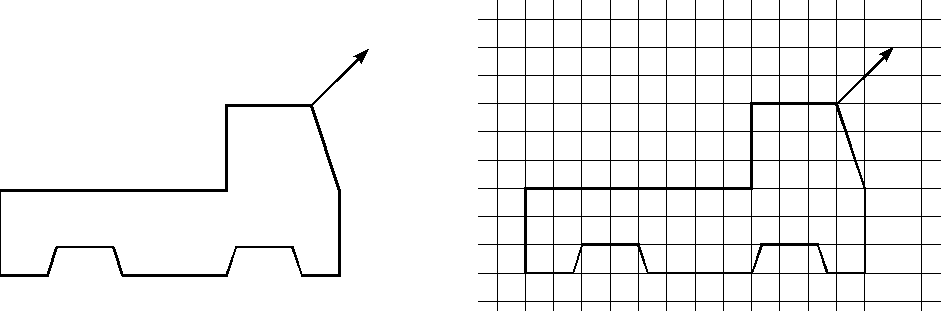
Anwendung: Herstellung anschaulicher Schrägrißbilder (am besten in einem Raster!)

(Vgl. Kapitel "Ähnlichkeit" und Beispiele in den Übungen.)

E. Drehung, Schiebung, Spiegelung als Kongruenzabbildungen

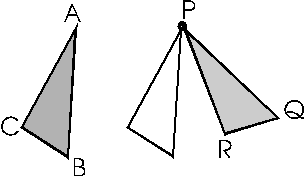
Ob eine Umklappung oder eine Bewegung stattgefunden hat, wenn zwei zueinander kongruente Figuren vorliegen, lässt sich am Umlaufsinn der Figuren erkennen.

Durch welche Abbildung kann das Dreieck A'B'C' jeweils aus dem Dreieck ABC hervorgegangen sein?

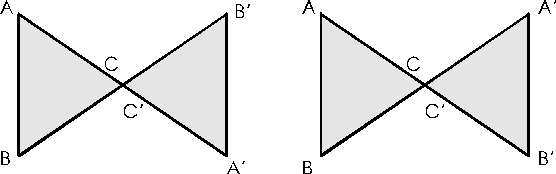
Haben beide Figuren denselben Umlaufsinn, dann spricht man von

gleichsinniger Kongruenzabbildung, sonst von gegensinniger.

Die linke Figur stellt einen Spezialfall einer Drehung, nämlich für den Drehwinkel ....... ° dar.

Statt die Drehung tatsächlich auszuführen, lässt sich gleich eine Spiegelung am Zentrum, eine sogenannte Punktspiegelung durchführen!

Eigenschaften:

* Das Zentrum Z ist Fixpunkt.

* Gerade durch Z sind Fixgerade.

* Punktspiegelung ist eine Involution.

* Jede Gerade und ihre Bildgerade sind zueinander parallel.

F. Beispiele für Verknüpfung von Abbildungen

Bei den diversen CAD-Programmen ist es kein Problem, eine gewählte Abbildung auch auf die Bildfigur anzuwenden, auf diese wieder usf. Diese Hintereinanderausführung der Abbildung heißt auch Verknüpfung der Abbildungen.

S_g o S_h [ g parallel zu h]

Durch die Hintereinanderausführung zweier Axialspiegelungen mit parallelen Achsen wird eine Schiebung festgelegt. Alle Schiebungspfeile sind zueinander parallel (normal zu den beiden Spiegelachsen), gleich lang (doppelt so lang wie der Abstand der beiden Spiegelachsen ist) und gleich orientiert.

PP" =

S_g o S_h [g nicht zu h parallel]

Die Hintereinanderausführung zweier Axial-spiegelungen mit schneidenden Achsen kann durch eine Drehung ersetzt werden. Das Drehzentrum ist der Schnittpunkt S, der Drehwinkel ist doppelt so groß wie der von den Spiegelachsen eingeschlossene Winkel.

S_g o T

Der Schiebungspfeil von T soll hier parallel zur Spiegelachse g sein.

Das Ergebnis dieser Art der Verknüpfung ist unter dem Namen GLEITSPIEGELUNG oder SCHUBSPIEGELUNG bekannt!

Diese Verknüpfung von Abbildungen stellt einen anderen Zugang zur Definition der Kongruenz dar:

Zwei Figuren F und F' heißen kongruent, wenn F' das Bild von F bezüglich einer Axial-spiegelung oder einer Verknüpfung endlich vieler Geradenspiegelungen ist.

Die Art und Zahl der anzuwendenden Abbildungen, um von F zu F' zu gelangen, ist nicht eindeutig.

G. Bandornamente

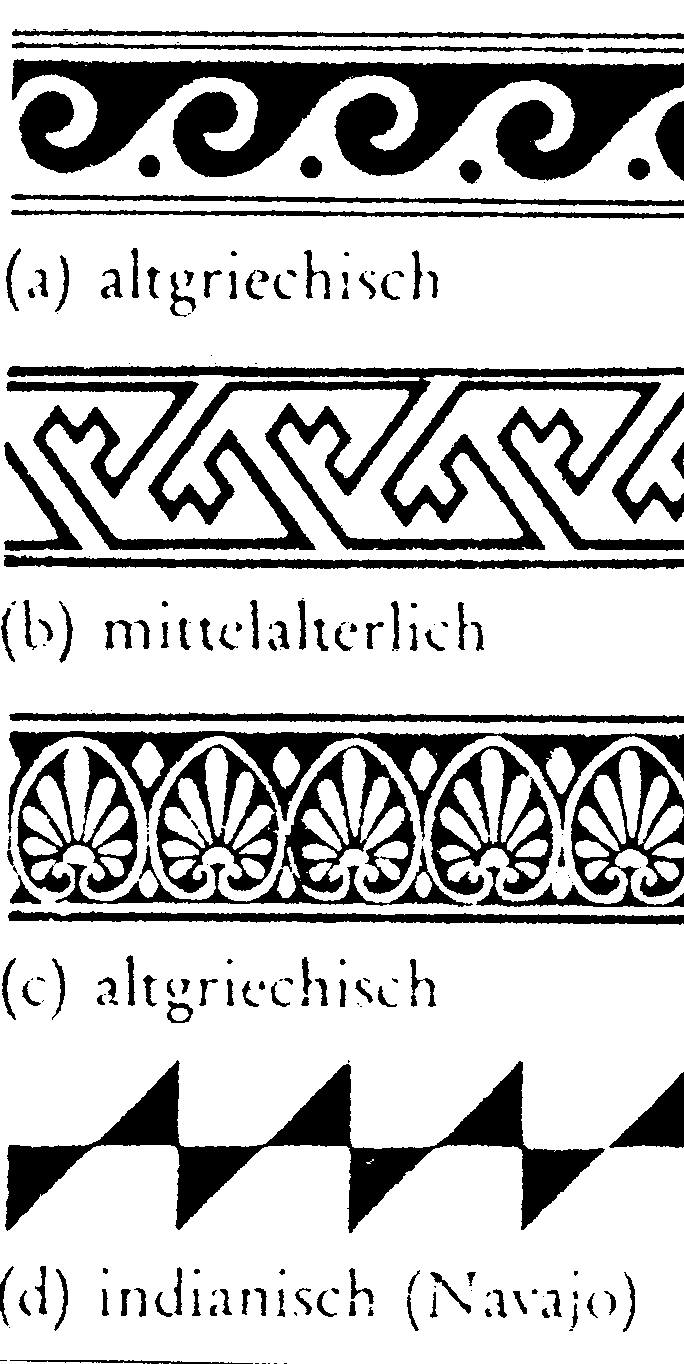
Die 7 Muster rechts unten stammen aus der Töperei San Ildefonso Pueblo in New Mexico Die Abbildung ist aus dem Buch von GARFUNKEL (Seite 182)

Unter einem Band- oder Streifenornament versteht man Figuren, die entstehen, wenn ein Motiv innerhalb eines Streifens nach beiden Seiten mit jeweils festem Abstand periodisch wiederholt wird. Da solche Ornamente in der Kunst vieler Kulturkreise (Stickereien, Tapetenmuster, Flechtmuster, Muster bei Töpferwaren schon bei prähistorischen Kulturen) auftreten, lohnt sich eine nähere Beschäftigung. Es zeigt sich nämlich, dass es lediglich 7 Typen solcher Bandornamente geben kann. Dies nützen Archäologen, um Funde mit Bandornamenten (hauptsächlich Töpferwaren) näher zu beschreiben.

Lit.: WITTMANN Erich, Elementargeometrie und Wirklichkeit

Verlag Vieweg, 1987 (224ff)

GARFUNKEL Salomon (Hrsg.), Mathematik in der Praxis

Spektrum der Wissenschaft, (180 ff)

FLACHSMEYER/FEISTE/MANTEUFEL Mathematik u. ornamentale Kunstformen

Verlag Harri Deutsch, Deutsch Tb., Bd. 75; Frankfurt/Main 1990

Auf die 7 Typen kommt man, wenn man jene Abbildqngen sucht, die das (unendlich lange gedachte) Band in sich transformieren, für welche also das Ornament eine Fixfigur ist.

Abbildungen rechts aus: Peter S. Stevens , Handbook of Regular Patterns, Cambridge, MA 1981

Auf der folgenden Seite sind zu jedem Bandornament alle Kongruenzabbildungen zu finden, die das Ornament als ganzes unverändert lassen

T...Translation

Sh...Axialspiegelung um eine horizontale Achse

Sv...Axialspiegelung um eine vertikale Achse

P...Punktspiegelung (= Drehung um 180°)

G...Gleitspiegelung

H. Kongruenzsätze für Dreiecke

Geometrie beschäftigt sich mit dem Studium der Eigenschaften von Figuren. Diese lassen sich in Dreiecke zerlegen oder durch solche beliebig genau annähern. Um Aussagen über Kongruenz und Unterschiede von Figuren machen zu können, ist das rasche Erkennen der Kongruenz von Dreiecken (und das Begründen derselben) wichtig.

In welchen Angabestücken müssen Dreiecke übereinstimmen, damit sie kongruent sind?

Diese Fragestellung ist gleichwertig mit der Frage nach den Angabestücken, die man benötigt, um ein Dreieck eindeutig konstruieren zu können!

Voraussetzen wollen wir:

Zwei Strecken sind kongruent, wenn sie in ihren Längen übereinstimmen.
Zwei Kreise sind kongruent, wenn sie in ihren Radien übereinstimmen.

Dann lassen sich die folgenden Sätze durch Konstruktion je zweier Dreiecke aus den gegebenen Abgabeelementen beweisen. Eine andere Möglichkeit des Beweises besteht darin, Kongruenzabbildungen zu suchen, die die beiden Dreiecke ineinander überführen. (Vgl. etwa WITTMANN 1987, Seite 87ff)

SSS-Satz

Haben zwei Dreiecke drei paarweise maßgleiche Seiten, so sind sie kongruent.

Beweis:

(z.B. nach der zweiten Methode) Voraussetzung: AB = PQ, BC = QR, CA = RP Zu zeigen: Es gibt eine Verknüpfung von Axialspiegelungen, sodass ABC ® PQR 1. Abbildung, z.B.TRANSLATION (A® P) 2. Abbildung, z.B.DREHUNG (um A'=P,B"=Q) 3. Abbildung (, falls C" ¹ R): SPQ

SWS-Satz

Stimmen zwei Dreiecke in den Maßen zweier Seiten und des von ihnen eingeschlossenen Winkels überein, so sind sie kongruent.

WSW-Satz

Stimmen zwei Dreiecke in den Maßen einer Seite und den ihnen anliegenden Winkeln überein, so sind sie kongruent.

Manchmal wird unter dieser Liste auch der SWW-Satz angeführt, den man aber durch Berechnung des dritten Winkels (Winkelsumme 180o)auf den WSW-Satz zurückführen kann.