Zur Übersicht

1. Kreis als Ortslinie

Erste Möglichkeit einen Kreis als Ortlinie zu definieren:

Ein Kreis (Kreislinie) ist die Menge aller Punkte, die von einem gegebenen Punkt ............... Abstand haben.

Grundbegriffe

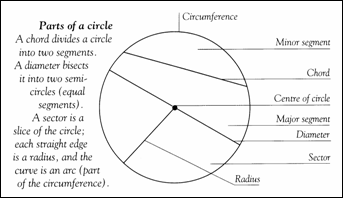
Ordne zu:

&xnbsp;t........Tangente (einzeichnen)

&xnbsp;sek....Sekante

&xnbsp;se......Sehne

p.......Passante

&xnbsp;z.......Zentrale

&xnbsp;d.......Durchmesser

&xnbsp;b.......Bogen

&xnbsp;Sek....Sektor

&xnbsp;Seg....Segment

&xnbsp;

Eine andere Möglichkeit, einen Kreis als Ortslinie zu definieren:

Kreis und Winkel

Gegeben ist eine Sehne AB; X sei ein beliebiger Punkt auf dem Kreis ("auf der Kreislinie") über AB; dann gilt: Die Größe des Winkels, den die von X ausgehenden Strecken zu A und B einschließen ist unabhängig von der Wahl des Punktes X.

 

Peripheriewinkel b

 

Zentriwinkel a

Beweisidee: Man nützt die Tatsache, dass alle drei Punkte A,B und X auf dem Kreis um M liegen, es enstehen gleichschenkelige Dreiecke, deshalb kann man etwas über das&xnbsp; Verhältnis der Basiswinkel&xnbsp; in A und B&xnbsp; bzw. X&xnbsp; zum Winkel am Scheitel M dieser Dreiecke&xnbsp; aussagen.

Eigentlicher Beweis:

1)      Zentriwinkel a

2)      Peripheriewinkel b

3)      Wieviele gleichschenkelige
         Dreiecke sind entstanden?

          Basiswinkel:

4)      Berechnung der 3 Zentriwinkel in&xnbsp; M

 

 

5)      Summe der drei Zentriwinkel:

Bemerkung 1: Dass der Winkel&xnbsp; über der Sehne AB und der Winkel unter derselben Sehne zueinander supplementär sind, wird in den Übungen bewiesen.

Bemerkung 2:&xnbsp;b tritt auch als Winkel zwischen Tangente und Sehne in A auf!

&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp;&xnbsp; Warum?

Zusammenfassend lässt sich formulieren:

Satz vom Peripherie-und Zentriwinkel: Jeder Peripheriewinkel über derselben Sehne ist gleich groß, und zwar halb so groß wie der entsprechende Zentriwinkel.

Mit Hilfe dieses Satzes lässt sich folgende Aufgabe lösen, die bei Vermessungsbeispielen eine Rolle spielt:

Gegeben sei eine Strecke AB, gesucht ist der Ort aller Punkte, von denen aus diese Strecke unter einem bestimmten Winkel erscheint.

Beispiel: Der Sehwinkel, unter dem AB gesehen wird, soll 60° sein. Zur Konstruktion von M beachte man die Bemerkung zur vorigen Figur!

 Zeichnung dynamisch

Damit können wir Kreisbögen mit Hilfe von Winkeln als Ortslinien definieren:

Die Menge aller Punkte, von denen aus eine gegebene Strecke ............... ............................................................ liegt auf&xnbsp; zwei Kreisbögen, die symmetrisch zur gegebenen Strecke liegen und den gegebenen Winkel als Peripheriewinkel besitzen.

Beispiel:
Alle 100 Meter gibt es an der Donau Markierungssteine, die die Entfernung zur Flussmündung angeben. Um den eigenen Standort am linken Treppelweg auf einer Skizze genauer ermitteln zu können, misst man als Sehwinkel zwischen zwei&xnbsp; x&xnbsp; (z.B. 600)&xnbsp; Meter voneinander entfernten Steinen am gegenüberliegenden Ufer den Winkel
b&xnbsp; = 75°.&xnbsp; Konstruiere die Lage des eigenen Standortes.


"Analogbeispiel"

geg: c = 8 cm,&xnbsp;&xnbsp; hc&xnbsp; = 5 cm, g = 75°

 

 

 

 

 

Sonderfall: Der Peripheriewinkel ist ein rechter Winkel

Satz von THALES:
Alle „Randwinkel“ im Halbkreis sind rechte Winkel.





Thales von Milet, um 600 v.Chr.

 

Wie lässt sich nun ein ganzer Kreis als Ortslinie mit Hilfe von Winkeln definieren?&xnbsp; ...

Anwendung:

Tangente aus einem&xnbsp; Punkt an einen Kreis

 

 

Zum Inhaltsverzeichnis